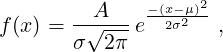1. The Normal Distribution

(40 pts.) In this problem, you will check if your values for the pendulum period T appear to follow a normal distribution (see Taylor, section 5.3.)

Unfortunately, while Mathematica can make nice histograms, it is a bit cumbersome to import the data and do the curve fitting. See the pendulum-period.nb and randerrors.nb notebooks on the course web site for a way to import your data into Mathematica and perform the fit to the normal distribution.

a.

Produce a histogram of your data. You may have to select a bin size and range manually. Try to pick them so that you get a reasonably smooth histogram. Do not print the histogram just yet—you will do so in step d. below.

b.

The normal distribution is defined as

(1)

where μ is the mean value and σ is the standard deviation. (If your histogram were normalized, you would get A = 1, but since it is not normalized, you need to include a scaling factor A.

Does your histogram resemble a normal distribution qualitatively? Discuss any significant differences.

c.

Perform a fit of Eq. 1 to your data. Note that Mathematica probably won’t get a good fit by default. You may have to supply the NonlinearModelFit function with initial guesses for μ and σ. Report your results for the fit parameters, along with their uncertainties.

d.

Make a graph showing the histogram data along with your fit to Eq. 1. Print out the graph to include with your homework.

e.

Compare the results from the statistical analysis and your curve fit. Does your mean value for T agree with the location of the peak of the histogram?

f.

Does your standard deviation agree with the width (i.e. σ) of the histogram? Though they likely won’t be identical for your data, they ought to be reasonably close to each other.

g.

Are there any visual features of your histogram that might help explain any discrepancies?

2. The Physical Pendulum

(20 pts.) In the simple pendulum lab, we assumed that the pendulum was a point object of mass M located a distance L away from the pivot point. In reality, however, a better model would be a cylinder of height h with the center of a cylinder a distance L away from the pivot point. Was this an important issue? Specifically,

a.

Look up the formula for the “physical pendulum”. Use that formula to calculate g in terms of the moment of inertia I.

b.

For a point mass, the moment of inertia would just be I_pt = ML². For the cylinder, it is more complicated. What is the moment of inertia I_cyl for the cylinder about the pivot point? You will probably find it useful to look up the “parallel axis theorem.”

c.

Find a formula for the difference between g_pt using the moment of inertia for a point mass and g_cyl using the moment of inertia of the cylinder about the pivot point.

d.

Analytically expand your difference formula assuming h ≪L, and keeping only the leading term.

e.

Put in your numerical values. How big is the difference between g_pt and g_cyl?

f.

Was this an important issue? Make specific reference to your quantitative results (including uncertainty) from your lab report.

g.

Of course the pendulum was not exactly a cylinder either. There were small additional masses at the top and bottom. Without doing any further calculations, do you think this would be an important further avenue of investigation? Why or why not?

General Homework Instructions

• Problems will be due at the beginning of class. Late homework will normally not be accepted.

• For written homework, I expect your work to be clearly organized and easy to follow. You should include not just numbers and calculations, but also include some text to explain what you are doing and why. This can often be quite brief, but it is your responsibility to make your reasoning clear; it is not the reader’s responsibility to try to figure out what you meant. Homework that is incomplete or difficult to understand will not get full credit. These guidelines are intended to help you present your work effectively.

  1.

  Be sure to include your name on each page.

  2.

  Each problem should be clearly labeled.

  3.

  It is often helpful to include figures. Any figures should have clear labels.

  4.

  Show your work clearly, and include all non-trivial steps. Use words to explain what you are doing and why. This can often be very brief, something like “Expand for small x” or “Use conservation of energy.”

  5.

  Allow plenty of space.

  6.

  Put a box around your final solution, including correct units.

• Illegible papers will not be accepted. If I have difficulty reading or understanding your work, I may return it to you ungraded for re-submission. You may resubmit a legible version (along with the original) by the next class meeting, but that version must not have any new content—it must simply be a legible version of the original.

• Please look at the homework problems ahead of time and ask questions about them either in or out of class. I am happy to give whatever help you need, but it is important that you eventually learn to do these sorts of problems on your own.

Academic Honesty

If you get bogged down with any of the problems, do not hesitate to discuss them with your instructor or with a fellow student. For this course–and indeed for most advanced courses in any discipline—I believe such collaboration to be an essential element for success. I do not require any specific or explicit group work, but my expectation is that everyone will be open to both giving and receiving aid from their peers.

The only stipulation is that if you get help from anyone (besides your instructor) you should acknowledge that collaboration. Please see the Academic Honesty policy for more information about appropriate and inappropriate collaboration.