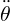
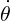
Physics 238—Intermediate Physics Lab
Homework Assignment #4
Due Monday, April 21, 2025, 1:15 p.m.
In this assignment, you will explore the relation between the width of a resonance peak and the lifetime of a damped oscillator.
To start, consider the decaying oscillations of a damped torsional oscillator. The differential equation for a damped, torsional oscillator of torsional constant κ and rotational inertia I is
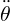 | = -ω02θ - γ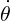 |
where ω0 = 2πf0 = 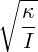 is the natural (undamped) frequency of the oscillator, and γ is a
term proportional to the drag, with units of rads-1. If released from rest from an initial angle θ0,
the resulting motion is a damped oscillation:
is the natural (undamped) frequency of the oscillator, and γ is a
term proportional to the drag, with units of rads-1. If released from rest from an initial angle θ0,
the resulting motion is a damped oscillation:
| θ(t) | = θ0 e-γt∕2 cos(ω vt + ϕ) . |
For this assignment, the key observation is to note that the amplitude decays exponentially:
| A | = θ0e-γt∕2 = θ 0e-t∕(2τ) |
where τ = 1∕γ is the time constant, or lifetime, associated with the motion. Recall that the energy of a simple harmonic oscillator is proportional to the amplitude squared, so we can also describe the decay in terms of energy:
| A2 | = E = E 0e-γt = E 0e-t∕τ | (1) |
If periodic forcing at frequency ωd is added, the new differential equation is
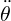 | = -ω02θ - γ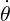 + α
0 sin + α
0 sin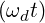 |
where α0 = 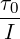 is the amplitude of the driving. After an initial transient, the steady state
motion is given by a sinusoidal oscillation with an amplitude θ0 given by
is the amplitude of the driving. After an initial transient, the steady state
motion is given by a sinusoidal oscillation with an amplitude θ0 given by
| θ0 | = 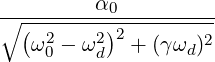 |
As with the decaying oscillation, the energy is related to the amplitude squared
| θ02 | =  | (2) |
In this assignment, you will explore the relation between the lifetime τ of the damped oscillations and the width of the peak in Eq. 2. Throughout, it will be simpler to leave things in terms of ω and γ (or τ), rather than using f and Q.
Hint: Assume that the damping is small, so that γ ≪ ω0 (or equivalently Q ≫ 1) so that you may drop higher order terms in γ∕ω0, and use the binomial expansion when appropriate.
Assignment 1: What frequency ωd gives the maximum for θ02 in Eq. 2? Call that frequency ωp. What is the magnitude of θ02 at that frequency?
Assignment 2: What are the two frequencies that give an amplitude in Eq. 2 equal to one half of that maximum? Only keep terms up to the lowest order in γ∕ω0.
Assignment 3: Define the full width at half maximum—FWHM—as the difference between the two frequencies you found in assignment 2. Find the relation between the FWHM and τ in Eq. 1.
Assignment 4: Test your prediction for your mechanical resonance curve for the torsional
oscillator. Note that since you measured amplitude θ and not θ2, you will measure the FWHM by
noting the frequencies at which your curve is at a height of 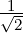 of the maximum. Note too that
you measured linear frequencies f, not angular frequencies ω, so you will need to manually
handle the factor of 2π.
of the maximum. Note too that
you measured linear frequencies f, not angular frequencies ω, so you will need to manually
handle the factor of 2π.
Assignment 5: Test your prediction for your electrical resonance curve for the RLC oscillator.
Again, you will actually need to measure the frequencies at which your curve is at a height of 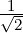 of the maximum, and compensate for factors of 2π.
of the maximum, and compensate for factors of 2π.
Your result should illustrate a quite general relation between the width of a resonance curve and the lifetime of the corresponding state.