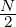 mp +
mp + 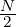 me ≈
me ≈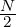 mp, since electrons are much less massive than
protons.
mp, since electrons are much less massive than
protons.
Physics 335—Thermal Physics
Homework Assignment #2
Revised Due Date: Friday, September 13, 2024, 11:40 a.m.
Problems 1.48 (held over from HW #01), 1.51 and 1.55 (20 pts. each).
Problems 2.3, 2.6, 2.8, and 2.11 (20 pts. each).
Hints: For problem 1.55, don’t derive anything for part (d), but do use that result in part (e). In
part (e), note that the total number of particles N consists of N∕2 protons plus N∕2 electrons.
The total mass is then M = 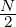 mp +
mp + 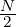 me ≈
me ≈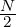 mp, since electrons are much less massive than
protons.
mp, since electrons are much less massive than
protons.
For the chapter 2 problems, feel free to use the posted Mathematica notebooks to get started, but note that direct enumerations of microstates for large numbers of items will exhaust Mathematica’s memory. You will need to use the combinatoric formulas instead. For any graphs, a simple ListPlot is fine; don’t worry about making a bar chart as in Fig. 2.4.
Problem 2.6 is very short.
For problem 2.11, note that the multiplicity is not given by Eq. 2.9. In contrast to the Einstein solid, each site can only hold either 0 or 1 energy units. In this case, the number of energy units q is simply equal to the number of down spins N↓. Look back at the end of section 2.1 for how to determine the multipicity in this case.