Ch 6:

Problem 6.10, 6.18, 6.20 (skip (d) and (e)), and 6.21.

Hints:

• For Problem 6.18, note that the heat capacity is simply .

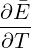• For Problem 6.20, note that parts (d) and (e) were included on the first take-home test. (That means you can skip them here.)

• For Problem 6.21, Mathematica’s ability to do symbolic calculations is very helpful. For example, suppose you had a trivial system with two energy levels, E₁ and E₂. You could have Mathematica calculate the partition function and average energy easily with the following commands:

                Z[\[Beta]_]  := Exp[-\[Beta] E1] + Exp[-\[Beta] E2]
                Ebar[\[Beta]_] = -D[Z[\[Beta]], \[Beta]]/Z[\[Beta]]
  

  To express the result in terms of T rather than β, you can use a substitution rule to create a new function of temperature:

                EbarT[T_] = Ebar[\[Beta]] /. \[Beta] -> 1/(k T)
  

  Then once you have the energy as a function of temperature, you can easily compute the heat capacity by taking another derivative.

  In this problem the partition function is longer and more complicated, but the basic structure of the problem is the same.

All problems are worth 20 pts. each.