Problem 7.28 (40 pts.) In addition, there will be three Physics colloquia in the last week of class that you are encouraged to attend. Colloquium attendance will be worth 10 extra credit points each.

Hints:

• Problem 7.28:

  • You may find it easier to do part (b) first and find the density of states g(ϵ) for the two-dimensional electron gas. You should find that g(ϵ) is a constant,

    

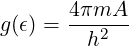
  • Once you have the density of states, it is easy to calculate N and U. Note, for example, that at T = 0,

    N = ∫ 0ϵF g(ϵ)dϵ
    U = ∫ 0ϵF ϵg(ϵ)dϵ

    The first equation means that you can rewrite g(ϵ) = .

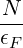  • You may skip part (c). At T = 0, μ = ϵ_F . At low, but non-zero temperature in 2 dimensions, it turns out that μ is still ϵ_F .

  • For part (d), note that the chemical potential is effectively defined by Eq. 7.53 for a given N and T. Part (d) involves a messy integral. If you define

    

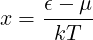
    then you should have an integral which evaluates to

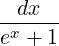    ∫ x0∞ = ln(1 + e-x0 )

    (If you want to prove that result, multiply the top and bottom by e^-x, and then make the substitution y = 1 + e^-x. Or you could just use the result given above.)

  • For part (e), you should get a result that looks similar to Eq. 6.93, but you need to replace the ratio 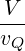by an analogous result for 2 dimensions: .
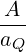