Mathematical Methods in Physics
Phys 314, Fall 2025
Resources and Demos Page





Hugel 020
Physics Department
Lafayette College
730 High St.
Easton, PA 18042
Phone: (610) 330-5207
Email: thomasbd@lafayette.edu

Other Phys 314 Course Pages
- Course Web Page
- Course Moodle
Physics References
- Lecture notes: Slightly Disturbed: Oscillations, Waves, and the Mathematics Behind Them, by Brooks Thomas.
Mathematics References
- Mathematical Methods for Physicists, 7th Ed., by George B. Arfken, Hans J. Weber, and
Frank E. Harris.
- Wolfram MathWorld: An online mathematics reference from the makers of Mathematica.
- List of Trigonometric Identities: A Wikipedia page which lists a variety of basic trig identities.
Programming References
- Mathematica
- Python
- Anaconda Download Page: Page from which you can download the Anaconda distribution of Python. The Python 3.9 version of Anaconda will be the "official" distribution we'll be using both in the lecture and lab sections of this course.
- The Python Tutorial: A tutorial on programming in the Python language from the official Python website.
- Matplotlib Site: The official site for matplotlib, the plotting library that I recommend using for creating plots in Python. The site includes links to official and unofficial documentation, examples, and tutorials.
Video Demos
- Simple Harmonic Oscillator
- Spray-Paint Oscillator:
A can of spray paint attached to a pair of springs oscillates up and down and traces out a sine wave on a roll of
paper.
- Power Series
- Taylor Polynomial Graphs:
Applet which allows you to plot a function f(x) alongside an nth-order Taylor-series approximation for that function around an arbitrary value of x, where n can be as high as n = 30.
- Complex Numbers
- Circular and Harmonic Motion:
Demonstration showing a ball attached to a rotating disk and evolving around its center next to a ball oscillating up and down at the end of a vertical spring. The projection of the shadow of the revolving ball on a screen lines up with the shadow of the oscillating ball. This illustrates the similarity between circular and simple harmonic motion that allows us to analyze the trajectory of the oscillating ball by "complexifying" it.
- Ordinary Differential Equations
- Magnetically Damped Oscillator:
Demonstration showing the underdamped, overdamped, and critically damped regimes for the harmonic motion of a pendulum consisting of a ruler with a magnet attached to the free end. The motion of the pendulum is damped by eddy currents induced in a nearby metal plate. The distance between the plate and the magnet is adjusted in order to vary the damping.
- Driven Mechanical Oscillator:
A mass on a spring is atached to a curved rod which is moved up and down by an electric motor. The amplitude of oscillation is dramatically larger when the motor drives the rod at the resonant frequency of the system.
- Resonant RLC Circuit:
A variable capacitor, large solenoid, and a 200 W light bulb are connected in series to an 120 V AC power supply. The inductance of the solenoid can be varied by adjusting the position of an iron core inside it (or removing the core altogether), and the capacitance can be varied by flipping a set of switches. The inductance and capacitance are varied. When the natural frequency of this LRC circuit is adjusted so that it is in resonance with the driving frequency supplied by the power supply, the current is maximized and the light bulb glows brightly.
- Coupled Differential Equations
- Coupled Air Carts:
Several demonstrations involving various numbers of carts coupled together by springs on an air track.
- Mode Shapes for Multiple Degree-of-Freedom Oscillators:
Denomstration of the normal modes for the transverse oscillations of a sets of up to four masses coupled together by springs.
- Slope and Direction Fields:
An applet, courtesy of Darryl Nester, which plots slope and direction fields for individual ODEs and systems of ODEs. It can only handle first-order ODEs, but of course you can formulate a higher-order ODE as a system of lower-order ODEs. Clicking on the state-space plot will create a curve which shows the trajectory along which the system evolves from that point. In other words, the pair of values corresponding to the point that you clicked on are taken as the initial conditions for the dependent variables. Clicking on the "Initial Points" button will show you a drop-down window with a button on it which allows you to clear all curves. Clicking on the "Timeplot" button will show you plots of each of the dependent variables as functions of the dependent variable for the trajectory curve you've most recently created.
- Lotka-Volterra Simulation:
An interactive simulation of the the Lotka-Volterra system of equations for a predator-prey system in which you can change the initial predator and prey populations and the parameters which govern the dynamics.
- Double Pendulum:
Demonstration of the chaotic behavior that can arise in a coupled double-pendulum system.
- Vector Calculus
- Divergence and Curl of Vector Fields:
An interactive demo in Desmos that allows you to view the divergence and curl of a vector field in two dimensions at different points in the plane.
- Line Integrals and Vector Fields:
An interactive demo in Desmos that allows you to evaluate the line integral along an arbitrary path through a vector field in two dimensions.
Fourier Analysis
- Fourier Series Applet:
Applet which show you the Fourier coefficients for arbitrary periodic functions and plays the corresponding waveform as a sound wave.
- Partial Differential Equations
- Wave Equation:
Simulation, courtest of VisualPDE, of the displacement, given as a function of position, within a two-dimensional medium within which the displacement evolves according to the two-dimensional version of the wave equation. Click on the "interactive simulation" link to start the simulation after you read the instructions.
- Heat Equation:
Simulation, courtest of VisualPDE, of the temperature, given as a function of position, within a two-dimensional medium within which the diffusion of heat is governed by the two-dimensional version of the heat equation. Click on the "interactive simulation" link to start the simulation after you read the instructions.
PhET Interactive Simulations
- Fourier Analysis
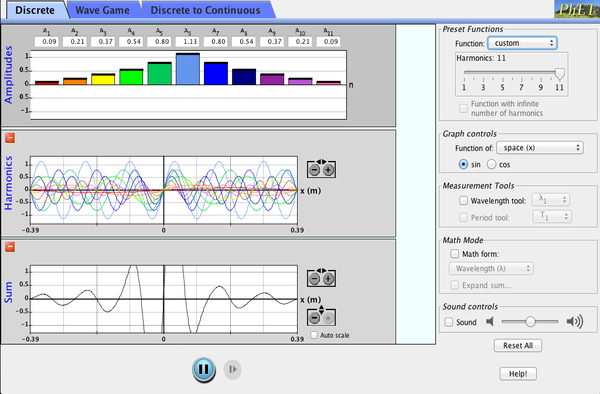
- Fourier: Making Waves
- Waves
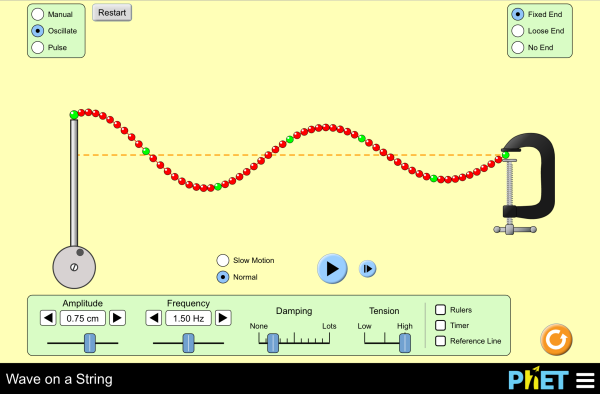
- Wave on a String